মানসপ্রতিম দাস

তারিখ লেখার পদ্ধতি এক-এক জায়গায় এক-এক রকম। সাধারণভাবে আমরা প্রথমে লিখি দিনটিকে, ১ থেকে ৩১ অবধি কোনও একটি সংখ্যা। তার পরে আসে মাস, সেখানে সংখ্যাটি ১ থেকে ১২-র মধ্যে। উল্টেও লেখেন কেউ-কেউ, অর্থাৎ মাস আসে দিনের আগে। সেই পদ্ধতি অনুসরণ করলে নভেম্বর মাসের ২৩ তারিখ লেখা যেতে পারে এভাবে– ১১|২৩। মাসের জায়গায় ১১ আর দিনের জায়গায় ২৩। খেয়াল করে দেখুন তো, কোনও একটা নকশা তৈরি হয়ে গেল কি না? রয়েছে পরপর চারটে সংখ্যা– ১, ১, ২, ৩। পরপর দুটো সংখ্যা যোগ করলে পাওয়া যায় পরের সংখ্যাটি। ১+১ = ২, ১+২ = ৩। এরকম সংখ্যার সারি পাওয়া গিয়েছিল দ্বাদশ-ত্রয়োদশ শতকের এক গণিতবিদের লেখায়, নাম তাঁর লিওনার্দো বোনাচ্চি (১১৭০-১২৪০)। তিনি অবশ্য বেশি পরিচিত অন্য একটা নামে– ফিবোনাচ্চি। তারিখের কথা বলতে গিয়ে এসে পড়লেন এই লিওনার্দো। আবার তাঁর প্রসঙ্গেই এসে পড়বেন অন্য কালের অন্য এক লিওনার্দো। আসবে তাঁর এক যুগান্ত-সৃষ্টিকারী ছবির কথা।

ছবিটিকে বলা হয় আর্ট ও সায়েন্সের মেলবন্ধন। রেনেসাঁস যুগের এক অসামান্য নিদর্শন। ১৪৯০ সালে এই ছবি এঁকে লিওনার্দো দ্য ভিঞ্চি (১৪৫২-১৫১৯) মানুষের অবয়বকে সবার কাছে উপস্থিত করেছিলেন এক ভিন্ন আলোয়। ছবির নাম ‘দ্য ভিট্রুভিয়ান ম্যান’। তিনি মানুষের শরীরের বিভিন্ন অংশের দৈর্ঘ্য মেপে সেগুলোর মধ্যে অনুপাত বের করেছিলেন। ছবির মধ্যে এমন স্পষ্ট করে অনুপাত নির্দেশ কেউ করেননি লিওনার্দোর আগে। লিওনার্দো জানান যে, প্রসারিত হাতের এক প্রান্ত থেকে আরেক প্রান্ত অবধি যে দৈর্ঘ্য– তা মানুষটির উচ্চতার সমান। থুতনির নিচ থেকে মাথার একেবারে উপর অবধি যে দৈর্ঘ্য, তা মানুষের উচ্চতার আট ভাগের এক ভাগ। তবে কেবলমাত্র এইসব কেঠো তথ্যের জন্য প্রসিদ্ধি লাভ করেনি ছবিটি। ভিট্রুভিয়ান ম্যান মানুষকে একইসঙ্গে পার্থিব গণ্ডিতে এবং মহাবিশ্বের অসীমতায় প্রকাশ করে। সেখানেই এই চিত্রকলার অধিকার ভাবজগতে। আসলে দুটো ছবি বসানো রয়েছে, একটার উপর আর একটা। নগ্ন এক মানুষ দু’ দিকে দু’ হাত প্রসারিত করে ছুঁয়ে আছেন একটি বর্গক্ষেত্রের বিপরীত দু’টি বাহুকে। আবার ওই একই মানুষ পা দুটো ছড়িয়ে এবং প্রসারিত হাত দুটো সামান্য উপরে তুলে স্পর্শ করছেন এক বৃত্তের পরিধি। এই চৌকো বর্গক্ষেত্র আসলে পৃথিবীর প্রতিনিধি আর বৃত্ত সূচিত করছে মহাবিশ্বের অনন্ত প্রসারকে।

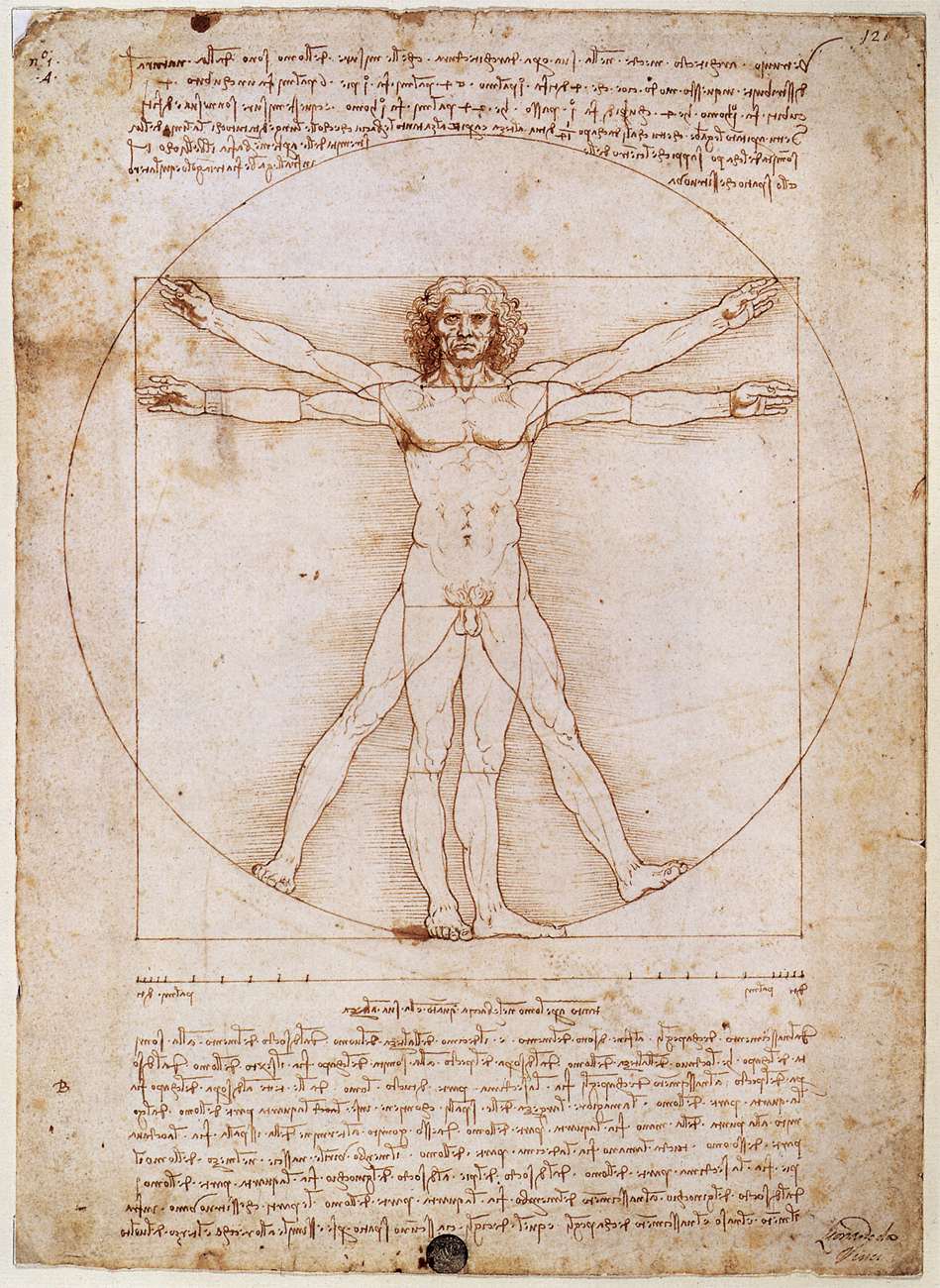
ছবির মধ্যে আবার অন্য একটা গণিত খুঁজে পেয়েছেন কিছু আলোচক। তাঁদের ধারণা যে ভিট্রুভিয়ান ম্যান আঁকতে গিয়ে ‘সোনালি অনুপাত’ (golden ratio) ব্যবহার করেছেন শিল্পী। সত্যিই কি শিল্পী এই অনুপাতকে ঠাঁই দিয়েছেন ছবিতে? তার আগে জানা উচিত কী এই অনুপাত? সংখ্যায় প্রকাশ করলে তার মান দাঁড়ায় ১.৬১৮। আসলে কাজ চলে যাওয়ার মতো করে, মানে ছোট করে লেখা হল অনুপাতের মানটা। আদতে দশমিক বিন্দুর পরে চলতেই থাকে এমন সংখ্যা, থামে না। এদের বলা হয় ‘অমূলদ’। যাক গিয়ে ওইসব খুঁটিনাটি, এসব আলোচনা করতে গিয়ে আমরা সরে যাচ্ছি ফিবোনাচ্চি নামে মানুষটা থেকে। ছবির আলোচনা মুলতুবি রেখে মনযোগ দেওয়া যাক তাঁর জীবনে। 

পিসার লিওনার্দো

মধ্যযুগে পশ্চিমি দুনিয়ায় সবথেকে মেধাবী গণিতজ্ঞ বলে পরিচিত ফিবোনাচ্চি জন্মেছিলেন পিসা প্রজাতন্ত্রে। সত্যি কথা বলতে কী, খুব বেশি তথ্য পাওয়া যায় না তাঁর জীবন সম্পর্কে। তবে এটা জানা যায় যে, তাঁর বাবা ছিলেন একজন ইতালীয় বণিক। কিছু প্রশাসনিক দায়িত্বও তাঁর সম্ভবত ছিল। বাবার সঙ্গে বহু জায়গায় ঘুরে বেড়িয়েছিলেন ফিবোনাচ্চি। তাঁর শিক্ষা শুরু হয় বুগিয়া নামে এক জায়গায় যা আজকের আলজিরিয়া-তে। এখানে তিনি জেনেছিলেন হিন্দু-আরব সংখ্যা-ব্যবস্থা সম্পর্কে। এদিকে সে যুগে দূর জায়গায় যাওয়ার জন্য পরিবহন হত জলপথে। ভূমধ্যসাগরের তীর বরাবর বাবার সঙ্গে ঘোরার সময় তিনি পরিচিত হন নানা দেশের বণিকদের সঙ্গে। শেখেন তাঁদের হিসেবনিকেশ, তাদের পাটিগণিত সম্পর্কে। বেশ বুঝতে পারেন যে, বণিকরা ত্যাগ করেছে রোমান সংখ্যামালা, হিসেবের সুবিধের জন্য বেছে নিয়েছে ১ থেকে ৯ অবধি সংখ্যা আর তার সঙ্গে শূন্যকে। হিন্দু-আরব সংখ্যা-ব্যবস্থায় প্রত্যেক সংখ্যায় একক, দশক, শতক ইত্যাদি স্থানমূল্য আছে। দশমিকের জায়গায় ১ থাকলে তার মূল্য হয় ১০, শতকের জায়গায় থাকলে সে মূল্য বেড়ে হয় ১০০– এইরকম। ১২০২ সালে ‘লিবের অ্যাবেসি’ নামে বই লিখলেন তিনি, জনপ্রিয় করলেন এই সংখ্যা-ব্যবস্থাকে। গোটা ইউরোপে দারুণ প্রভাব ফেলেছিল এই বই– সহজ আর দ্রুত করে দিয়েছিল ব্যবসা-বাণিজ্যের দরকারি গণনাগুলোকে। সম্রাট দ্বিতীয় ফ্রেডেরিক অঙ্ক আর বিজ্ঞান পছন্দ করতেন খুব। ফিবোনাচ্চির অবদানে মুগ্ধ হয়ে পিসা প্রজাতন্ত্রের পক্ষ থেকে ১২৪০ সালে তাঁর জন্য একটা মোটা অঙ্কের মাস-মাইনে বরাদ্দ করেন তিনি। 

‘লিবের অ্যাবেসি’ গ্রন্থের প্রথম সংস্করণ সংরক্ষিত নেই। তবে এটা জানা আছে যে ওই বইয়ের পাতায় খরগোশদের সংখ্যাবৃদ্ধি নিয়ে একটা আলোচনা করেন ফিবোনাচ্চি। নেহাৎই সংখ্যার কসরৎ, জীববিজ্ঞানের শর্ত থেকে মুক্ত সেটা। সবে জন্মানো একজোড়া খরগোশ, একটা পুরুষ আর একটা স্ত্রী, ছেড়ে দেওয়া হল মাঠে। এক মাস পর থেকে প্রজনন ক্ষমতা পাবে তারা। ফলে দ্বিতীয় মাসের শেষে একটা স্ত্রী-খরগোশ জন্ম দিল আরেক জোড়া খরগোশের। ধরে নেওয়া হল যে, কখনওই মারা যাবে না কোনও খরগোশ; আর জন্মের পর দ্বিতীয় মাস থেকে প্রজননে সক্ষম হবে তারা। এবার তাহলে জোড়ায় গুনলে মাস অনুযায়ী কত দাঁড়াবে খরগোশের সংখ্যা? জানুয়ারিতে ১, ফেব্রুয়ারিতেও ১, মার্চে ২, এপ্রিলে ৩, মে মাসে ৫, জুনে ৮– এইরকমভাবে বাড়বে ব্যাপারটা। এভাবেই তৈরি হয়ে গেল ফিবোনাচ্চির শৃঙ্খলা। কিন্তু স্রষ্টা ফিবোনাচ্চি যেটা ভাবতে পারেননি তা লুকিয়ে আছে তাঁর এই শৃঙ্খলায়। প্রথম দুটো ১ আর ২ সংখ্যাটা বাদ দেওয়া যাক। এরপর থেকে একটা সংখ্যাকে আগের সংখ্যা দিয়ে ভাগ করলে যা পাওয়া যায় সেটা সোনালি অনুপাতের খুব কাছাকাছি। শৃঙ্খলা যত এগবে, সংখ্যাগুলো যত বেশি বড় হবে ততই নিখুঁতভাবে বেরিয়ে আসতে থাকবে সোনালি অনুপাত। 

প্রকৃতিতে সোনালি অনুপাতের স্বাক্ষর 

সূর্যমুখী ফুলে বীজগুলো যেভাবে সাজানো থাকে, তার নির্দিষ্ট একটা নকশা যে থাকতে পারে, তা নিয়ে সংশয় থাকার কথা নয়। আমরা বলতেই পারি যে প্রকৃতি তার সদস্যদের জন্য নানারকম নকশা বরাদ্দ করে থাকে। কিন্তু তার মধ্যে সোনালি অনুপাত? সেটা স্বাভাবিকভাবে আন্দাজ করা সম্ভব নয়। আসলে নিজের প্রজাতির অস্তিত্ব সুনিশ্চিত করার জন্য বৃক্ষ চেষ্টা করে যত বেশি সম্ভব বীজ একটা নকশায় ঠেসে রাখার। কিন্তু যেমন-তেমন করে রাখলে তো হবে না, কোনও বীজই যেন ঢাকা না পড়ে তার বন্দোবস্ত থাকতে হবে এই সজ্জায়। তাই দেখা যায় যে ক্লক ও অ্যান্টিক্লক, দু’রকম সজ্জায় বীজেদের প্যাঁচালো গঠন (spiral) তৈরি হয় ফুলে। আবার স্পাইরালের প্রত্যেকটা শাখা কতটা পাক খাচ্ছে সেটাও গুরুত্বপূর্ণ। খুব বেশি বা খুব কম হলে চলবে না, দেখা যায় এই পরিমাণটা সোনালি অনুপাতের সমান। এটা বোঝার আর একটা পথ হল এইরকম– প্রত্যেকটা স্পাইরাল সমকোণে বা নব্বই ডিগ্রিতে একবার পাক খাওয়ার পর যতটা চওড়া হয়ে যায় তা সোনালি অনুপাতের সমান। 

বলা যায় অন্য ফুলের কথাও এবং সোনালি অনুপাত সরিয়ে রেখে সরাসরি আনা যায় ফিবোনাচ্চির বিখ্যাত শৃঙ্খলা ফুটে ওঠার কথা। ধৈর্য ধরে বহু ফুলের সমীক্ষা করলে দেখা যায় যে সেগুলোর পাপড়ির সংখ্যা ফিবোনাচ্চি শৃঙ্খলার কোনও একটা সংখ্যা– ৩, ৫, ৮ বা ১৩। বহু ফুলে দেখা যায় যে, ক্লক ও অ্যান্টিক্লক অভিমুখী পাপড়ির স্পাইরালের সংখ্যা ভিন্ন; কিন্তু ফিবোনাচ্চি সিরিজের মধ্যেই পাওয়া যায় সেগুলোকে। শুধু ফুলই বা বলি কেন, ফলের মধ্যেও তো আছে ফিবোনাচ্চি সিরিজের উপস্থিতি। আনারস, ফুলকপি, ব্রকোলির মধ্যেও খুঁজে পাওয়া যাবে ফিবোনাচ্চিকে। 

সংগীতে, শিল্পকলায় 

শাস্ত্রীয় সংগীতের মধ্যেও খুঁজে পাওয়া যাবে ফিবোনাচ্চি সিরিজ বা সেটার সঙ্গে সংশ্লিষ্ট সোনালি অনুপাতকে। মহান সুরস্রষ্টা মোৎজার্ট রচিত ‘সোনাটা’ দুটো ভাগে বিভক্ত– এমনভাবে ধরে নেওয়া যেতে পারে। পর্যায়সূচক দাগের (bar) সংখ্যা দ্বিতীয় ভাগে এমনই যে, প্রথম ভাগে দাগের সংখ্যা দিয়ে ভাগ করলে তা পৌঁছয় সোনালি অনুপাতের খুব কাছাকাছি। ইতালীয় গণিতবিদের শৃঙ্খলা থেকে অনুপ্রাণিত হয়ে এক ধরনের কবিতারও নাকি জন্ম হয়েছে– ফিব পোয়েট্রি। এমন একটা কবিতায় যদি ছ’টা পঙ্‌ক্তি থাকে তবে পরপর পঙ্‌ক্তিতে সিলেব্‌ল যে সংখ্যায় থাকবে তা হল– ১, ১, ২, ৩, ৫, ৮! 

চিত্রকলায় যে সোনালি অনুপাত এসেছে তার সংক্ষিপ্ত একটা আলোচনা তো হয়ে গিয়েছে শুরুতেই। বিশ্ববরেণ্য চিত্রকরদের মধ্যে লিওনার্দো দ্য ভিঞ্চি ছাড়াও এই অনুপাত ব্যবহারে আগ্রহ দেখিয়েছেন সালভাদর দালি। তবে এখানে বিপরীত কথাও আছে কিছু। সমালোচকদের অনেকেই বিশ্বাস করতে চান যে, লিওনার্দো বা দালি সচেতনভাবে ব্যবহার করেছেন সোনালি অনুপাত। জনপ্রিয় সাহিত্যেও বারবার উঠে আসে এই তত্ত্ব। ‘দ্য দা ভিঞ্চি কোড’ নামে বিখ্যাত বইতে ড্যান ব্রাউন ঠিক একই কাজ করেছেন। কিন্তু আধুনিক সময়ে বেশ কিছু বিশ্লেষণে যা উঠে এসেছে, তা এইসব আলোচকদের জন্য উৎসাহজনক নয়। যেমন– ‘ভিট্রুভিয়ান ম্যান’ নামের চিত্রকলায় বৃত্তের ব্যাসার্ধ এবং বর্গক্ষেত্রের বাহুর যে অনুপাত আনতে চেয়েছেন লিওনার্দো, তা সোনালি অনুপাত থেকে বেশ কিছুটা আলাদা। আসলে রোমান স্থপতি ভিট্রুভিয়াসের পরিকল্পনা থেকে উৎসাহ পেয়েছিলেন লিওনার্দো, সেই পথেই এগিয়েছিলেন তিনি। ভিট্রুভিয়াস যে সব শর্ত দিয়েছিলেন এই ছবির জন্য, তার মধ্যে একটা ছিল– বৃত্তের কেন্দ্র হতে হবে মানুষটির নাভিতে। আর একটি হল, হাতের আঙুলের ডগা এবং পায়ের প্রান্ত ছুঁয়ে যাবে বৃত্ত। কোনও কোনও বিশ্লেষক মনে করেন যে, এই শর্তগুলো নিখুঁতভাবে রক্ষা করা তত সহজ নয়। লিওনার্দোর ছবিও পুরোপুরি রক্ষা করতে পারেনি এই শর্ত। শর্ত রক্ষিত হলেই সোনালি অনুপাত দেখা দেবে এমন নয়, তবে সব মিলিয়ে ‘ভিট্রুভিয়ান ম্যান’-এ সোনালি অনুপাত খুঁজে বের করার ব্যাপারটা আলোচকের কল্পনার রঙে রাঙানো। অবশ্য সোনালি অনুপাত রক্ষা করবেন এমন মানসিকতা নিয়ে তুলি ধরেছেন অনেক শিল্পীই। কিছু ছবিতে দেখতে পাওয়া দুর্দান্ত স্পাইরালে সেই সৃষ্টি পাওয়া যাবে সহজে। 

আচার্যকে যেন না ভুলি

এতক্ষণ ফিবোনাচ্চি-বন্দনা করে এসে শেষে একটু ভিন্ন সুরে না-গাইলেই-নয়। সংখ্যার যে শৃঙ্খলার কথা নিয়ে আলোচনা হল তা ইউরোপীয় ভূখণ্ডে প্রথম চর্চা করেছেন ফিবোনাচ্চি– এটা সঠিক। তবে তাঁরও আগে এই শৃঙ্খলা আলোচিত হয়েছে ভারতের এক পণ্ডিতের রচনায়। খ্রিস্টপূর্ব দ্বিতীয় শতকে এই শৃঙ্খলার ধারণা আমাদের দিয়েছিলেন পিঙ্গল। তাঁর লেখা ‘ছন্দশাস্ত্র’ কবিতার মাত্রা বিচার করতে গিয়ে এসেছিল এই সিরিজ। সেখানে এই সংখ্যার পরম্পরাকে তিনি নাম দিয়েছিলেন ‘মাত্রামেরু’।

পিঙ্গল সম্পর্কে আমাদের অবহিত করেন বীরহাঙ্ক, সেটা ৬০০ থেকে ৮০০ খ্রিস্টাব্দের মধ্যে। তবে এ তো জানা কথা যে, ইতিহাসের বহু আবিষ্কার ভিন্নতর ভূখণ্ডে পুনরাবিষ্কৃত হয়েছে ভিন্ন কোনও পরিস্থিতি ও প্রেক্ষাপটে। এ ঘটনাকেও গ্রহণ করা যায় সেভাবেই। এখন, সিরিজ উপহার দেওয়ার ক্ষেত্রে ফিবোনাচ্চির অনুপ্রেরণার মধ্যে পিঙ্গলের কোনও ভূমিকা রয়েছে কি না তা বিস্তৃত বিতর্ক এবং আলোচনার বিষয়। তবে ভূমিকা থাকার সম্ভাবনা খুবই বেশি, কারণ ভারতীয় গণিতজ্ঞদের তৈরি সংখ্যা-ব্যবস্থা এতটা প্রভাবিত করেছিল যাঁকে, তাঁর পক্ষে আচার্য পিঙ্গলের প্রভাব এড়িয়ে যাওয়া সত্যিই কঠিন। সুতরাং নভেম্বর মাসের ২৩ তারিখের মধ্যে সিরিজের যে খেলা লুকিয়ে আছে– তাতে মুগ্ধ হওয়ার সময় ফিবোনাচ্চির সঙ্গে পিঙ্গলকে স্মরণ করাও আমাদের কর্তব্য।